F. Los números irracionales
-
Algunos campesinos que necesitaban calcular el número de semillas que necesitaban para sembrar sus campos. Para simplificar su trabajo, dividian el campo en triángulos, pues había fórmulas para calcular el área de un triángulo. A partir de aquí se desarrolló la trigonometría.
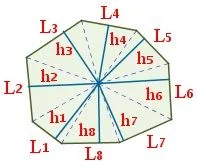
Cálculo de área con triángulos. -
Otros los hicieron con rectángulos. A partir de aquí se desarrolló el cálculo diferencial e integral.
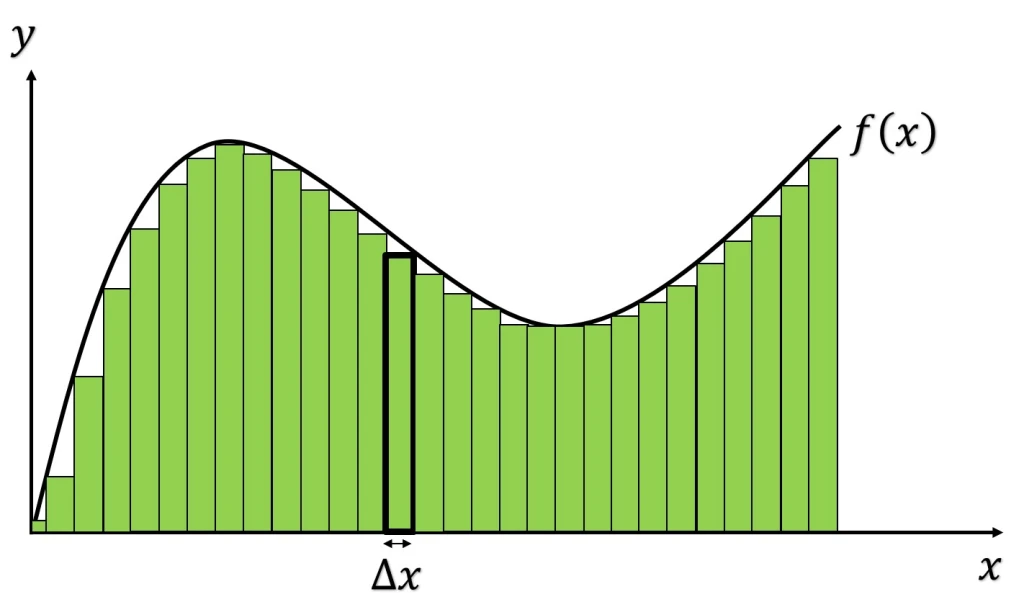
Cálculo de áre con rectángulos. -
Al estudiar los triángulos descubrieron que en los triángulos rectángulos, la suma de los cuadrados de cada cateto es igual al cuadrado de la hipotenusa.
-
Aunque este resultado se obtuvo en la antigua Babilonia (hoy Irak), llega a nosotros por medio de la escuela pitagórica de hace mucho, pero mucho tiempo, en lo que hoy es Grecia.
-
En el siguiente triángulo, a2 + b2 = c2.
De Marianov - Trabajo propio, CC0, Enlace -
La operación a2 = (a)(a). Por ejemplo, 32 = (3)(3) = 9.
-
Para poder obtener el valor de la hipotenusa, se desarrolló la raíz cuadrada, de tal forma que si a2 = b, entonces a = √b.
-
Se sabía que si a y b valen 1, el valor de c es √2.
-
Un miembro de la escuela pitagórica se dió cuenta de que √2 no se puede expresar como número racional; su escuela tenía como dogma que el Universo era perfecto y todo se podía expresar como números racionales. El descubridor murió; unos dicen que se suicidó y otros dicen que lo suicidaron en su escuela y sus miembros fingieron felicidad 🙄, aunque tenían el corazón partido 😢 y ocultaron este resultado al mundo 🤬, pero con el paso del tiempo todo el mundo se enteró de este resultado y no le importó.
-
Los matemáticos volvieron a ser felices 😁, pero hubo algo que les rompió el corazón 😢.
